ПР 10 Перевод чисел из десятичной системы счисления в другие системы счисления

Цель: Сформировать умение переводить числа из десятичной системы счисления в другие.

Теоретическая часть.

Система счисления - набор знаков, используемых для записи чисел и правила записи чисел. Эти знаки называются цифрами.

Набор этих цифр называется алфавитом системы счисления.

Различают позиционные и непозиционные системы счисления.

Если для каждого числа системы счисления выполняется правило: вес цифры (ее значе­ние) зависит от положения цифры в числе, такая система счисления называется позицион­ной. Если хотя бы для одного числа это правило не выполняется, система счисления называ­ется непозиционной.

Пример непозиционной системы счисления - римская. В ней для числа II вес каждой цифры одинаков (равен единице).

Количество цифр в позиционной системе счисления называется основанием системы счисления.

При записи чисел в различных системах счисления принято записывать основание систе­мы счисления справа внизу возле числа. Например, число 6 в восьмеричной системе счисле­ния записывают: 68. (Если основание системы счисления справа внизу возле числа не указа­но, считается, что это десятичная система счисления.)

Для перевода десятичного числа в другую систему счисления необходимо:

1)  делить нацело с остатком число на нужное основание системы счисления;

2)  получившееся частное (целое) тоже делить нацело с остатком на это основание;

3)  продолжать деления до тех пор, пока частное не получится меньше основания системы счисления;

4)  выписать последнее частное и остатки в порядке, обратном их получению

Перевод из десятичной системы счисления в двоичную:

Задача 1: Переведите число 25 из десятичной системы счисления в двоичную 

 25₁₀ _________₂

Делим с остатком на 2 до тех пор пока не получим частное 1.

25:2=12(ост 1)       12:2=6 (_ост 0)    6:2=3(ост 0)   3:2=1(ост 1)

На этом деление заканчиваем, т.к. 1 на 2 не делится нацело

Выпишем последнее частное и остатки в обратном порядке.  

Ответ: 25₁₀11001₂

 

Перевод из десятичной системы счисления в троичную,……, восьмеричную:

 Делим на то число, какое основание у новой системы счисления.

Например, для перевода в троичную систему делим на 3, для перевода в шестеричную систему делим на 6, для перевода в восьмеричную систему делим на 8.

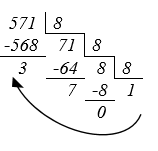
Задача 2: Переведите число 571 из десятичной системы счисления в восьмеричную

571₁₀ _________₈

Делим с остатком на 8 до тех пор пока не получим частное меньшее 8.

Выпишем последнее частное и остатки в обратном порядке.

Ответ: 571₁₀1073₈

 

Задача 3: Переведите число 357 из десятичной системы счисления в троичную

357₁₀_________₃

Делим с остатком на 3 до тех пор пока не получим частное меньшее 3.

Выпишем последнее частное и остатки в обратном порядке.

Ответ: 357₁₀111020₃

 

Задача 4: Переведите число 123 из десятичной системы счисления в шестеричную

123₁₀_________₆

Делим на 6 до тех пор пока не получим частное меньшее 6.

Выпишем последнее частное и остатки в обратном порядке.

Ответ: 123₁₀323₆

 

Перевод из десятичной системы счисления в шестнадцатеричную

Делим на 16 до тех пор пока не получим число меньшее 16.

Выпишем остатки в обратном порядке, учитывая, что цифра 10-A, 11-B, 12-C, 13-D, 14-E, 15-F.

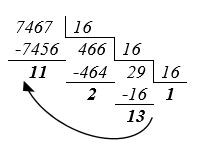 Задача 5: Переведите число 7467 из десятичной системы счисления в шестнадцатеричную.

7467₁₀_________₁₆

Делим на 16 до тех пор пока не получим число меньшее 16.

Выпишем остатки в обратном порядке,

заменив соответствующие остатки 13 на D и 11 на B.

Ответ: 7467₁₀1D2B₁₆

Практическая часть.

Переведите числа в указанные системы счисления.

По окончании урока сдайте тетрадь преподавателю для проверки вычислений.