ПР 14 Решение логических задач

 Цель: Сформировать представление о способах решения логических задач.

Теоретическая часть.

Метод рассуждений.

Для задач, в условии которых сказано, что часть утверждений персонажей ложна, а часть истин­на, удобно использовать метод рассуждений. Идея этого метода заключается в том, что дела­ется предположение об истинности одного из утверждений, и далее на основе этого предположе­ния анализируются остальные утверждения. Анализ остальных утверждений может привести к двум случаям - либо задача оказалась решена, либо встретилось противоречие. Если встрети­лось противоречие, это, означает, что первоначальная гипотеза об истинности одного из утвер­ждений была неверна, и это утверждение на самом деле ложно. Далее, с учетом этой информа­ции продолжаем анализ утверждений, пока не решим задачу.

Пример. На олимпиаде по информатике участвовали пятеро учеников: Андрей (А), Коля (К),
Виктор (В), Егор (Е), Степан (С). Об итогах олимпиады имеется пять высказываний:

1)    Второе место занял Андрей, а Егор оказался третьим.

2)    Выиграл Виктор, а Коля поднялся на второе место.

3)    Степан занял только второе место, а Виктор был последним.

4)    Все-таки на первом месте был Егор, а Коля был четвертым.

5)    Да, Коля был действительно четвертым, а Андрей вторым.

Если известно, что в каждом высказывании одно утверждение правильное, а другое нет, то кто занял второе место и на каком месте был Андрей?

Решение

Предположим, что в 1-м высказывании истинна первая половина (второе место занял Анд­рей), а вторая ложна, т.е. Егор - не третий. Заметим, что Егор и не второй, так как мы предположили, что это место занято Андреем.

Рассмотрим 2-е высказывание. Так как мы предположили, что второе место занял Андрей, значит утверждение и Коля поднялся на второе место и - ложно, а истинно - Выиграл Виктор.

Подведем промежуточные итоги. По нашей гипотезе Виктор - первый, Андрей -- второй, Егор - четвертый или пятый, Коля - третий, четвертый или пятый.

Перейдем к 3-му высказыванию. Виктор не может быть последним (из нашей гипотезы следу?
ет, что он цервый), следовательно, истинна первая половина высказывания «Степан занял только второе место» , но это противоречит нашей гипотезе, согласно которой на втором месте Андрей. Значит, гипотеза была неверна, а верна противоположная ей: в 1-м высказывании ложна первая половина, а вторая истинна. Таким образом, мы теперь достоверно знаем, что Егор занял третье место, а Андрей не второй и не третий.

Посмотрим, в каких высказываниях еще упоминается место Егора. В первой части 4-го вы­сказывания говорится, что Егор был на первом месте. Но мы уже точно знаем, что это неправ­да, значит, истинна вторая часть высказывания: «Коля был четвертым» .

Аналогично заключаем из 2-го высказывания, что Виктор - первый.

Далее из 3-го высказывания получаем, что вторым был Степан.

Итак, тройка лидеров выглядит следующим образом:

1.    Виктор

2.    Степан

3.    Егор

Из 5-го высказывания следует, что Коля был четвертым, следовательно, Андрею остается по­следнее место.

Ответ: Виктор-1место;Степан-2 место; Егор-3 место; Коля-4 место; Андрей- 5 место.

 

Табличный метод.

Более формализованным способом решения логических задач является метод таблиц.

Пример. В бюро переводов приняли на работу троих сотрудников - Диму, Сашу и Юру. Каждый из них знает ровно два иностранных языка из следующего набора - немец­кий, шведский, японский, китайский, французский и греческий, при этом каждым языком владеет только один переводчик.

Известно, что:

1.      Ни Дима, ни Юра не знают японского

2.      Переводчик со шведского старше переводчика с немецкого

3.      Переводчик с китайского, переводчик с французского и Саша родом из одного города

4.      Переводчик с греческого, переводчик с немецкого и Юра учились втроем в одном институте

5.      Дима - самый молодой из всех троих, и он не знает греческого

6.      Юра знает два европейских языка

В ответе запишите первую букву имени переводчика с шведского языка и через запя­тую первую букву имени переводчика с китайского.

Решение

Составим таблицу, в строках которой имена переводчиков, в столбцах - языки. Знание пере­водчиком языка будем отмечать единицей в соответствующей клеточке, незнание - нулем.

 Из 1-го условия:

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима			0
Юра			0
Саша

 

Дополним таблицу информацией из 2-го и 5-го условия:

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима		0	0			0
Юра			0
Саша

 

Дополним таблицу информацией из 3-го условия:

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима		0	0			0
Юра			0
Саша				0	0

 

Дополним таблицу информацией из 4-го условия:

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима		0	0			0
Юра	0		0			0
Саша				0	0

 

Из таблицы видно что, ни Дима, ни Юра не знают японского. Следовательно, его дол­жен знать Саша. Аналогично получаем, что Саша знает греческий.

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима		0	0			0
Юра	0		0			0
Саша			1	0	0	1

 

Поскольку каждый переводчик знает только два иностранных языка, в строке Саши остальные клетки заполняем нулями.

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима		0	0			0
Юра	0		0			0
Саша	0	0	1	0	0	1

 

Из таблицы видно, что Дима должен знать немецкий, а Юра - шведский

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима	1	0	1			0
Юра	0	1	0			0
Саша	0	0	1	0	0	1

 

Из 6-го условия получаем, что Юра не знает китайского. Из таблицы следует, что то­гда в качестве второго языка он должен знать французский.

 

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима	1	0	0			0
Юра	0	1	0	0	1	0
Саша	0	0	1	0	0	1

 

Окончательный вид таблицы:

	Немецкий	Шведский	Японский	Китайский	Французский	Греческий
Дима	1	0	0	1	0	0
Юра	0	1	0	0	1	0
Саша	0	0	1	0	0	1

 

Ответ: Ю,Д

Пример. Девять школьников, остававшихся в классе на перемене, были вызваны к директору. Один из них разбил окно в кабинете. На вопрос директора, кто это сделал, были получены следующие ответы:

Володя: «Это сделал Саша».

Аня: «Володя лжет!»

Егор: «Маша разбила».

Саша: «Аня говорит неправду!»

Рома: «Разбила либо Маша, либо Нина…»

Маша: «Это я разбила!»

Нина: «Маша не разбивала!»

Коля: «Ни Маша, ни Нина этого не делали».

Олег: «Нина не разбивала!»

Кто разбил окно, если известно, что из этих девяти высказываний истинны

только три? Ответ запишите в виде первой буквы имени

Решение:

1) Предположим, что окно разбил Саша. Обозначим за 1 - истину, а за 0- ложь. Получим первый столбец. Получили 5 истинных высказываний, что противоречит условию задачи. Значит наше предположение не верно.

2) Предположим, что окно разбила Маша. Получим второй столбец. Получили 5 истинных высказываний, что противоречит условию задачи. Значит наше предположение не верно.

2) Предположим, что окно разбила Нина. Получим третийстолбец. Получили 3 истинных высказываний, что соответствуетусловию задачи. Значит наше предположение верно. Окно разбила Нина.

 

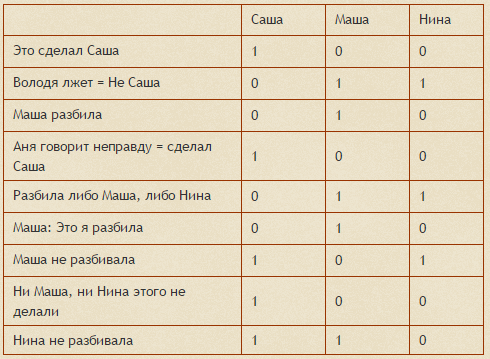
Ответ: [Н]

Схематичный метод.

Пример.На одной улице стоят в ряд 4 дома, в которых живут 4 человека: Алексей, Егор, Виктор и Михаил. Известно, что каждый из них владеет ровно одной из следующих профессий: Токарь, Столяр, Хирург и Окулист, но неизвестно, кто какой и неизвестно, кто в каком доме живет. Однако, известно, что:
1) Токарь живет левее Столяра
2) Хирург живет правее Окулиста
3) Окулист живет рядом со Столяром
4) Токарь живет не рядом со Столяром
5) Виктор живет правее Окулиста
6) Михаил не Токарь
7) Егор живет рядом со Столяром
8) Виктор живет левее Егора
Выясните, кто какой профессии, и кто где живет, и дайте ответ в виде заглавных букв имени людей, в порядке слева направо. Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, ответ был бы: КНРО

Решение:

Введем обозначения: А-Алексей, Е-Егор, В-Виктор, М-Михаил, Т-токарь, С-столяр, Х-хирург, О-окулист.

Начнем в первого условия и выпишем варианты, которые удовлетворяют ему (на рисунке ниже это первая строка). Далее будем накладывать следующее условие на выбранные варианты. И так будем делать до тех пор, пока не рассмотрим все условия. На рисунке описан ход решения:

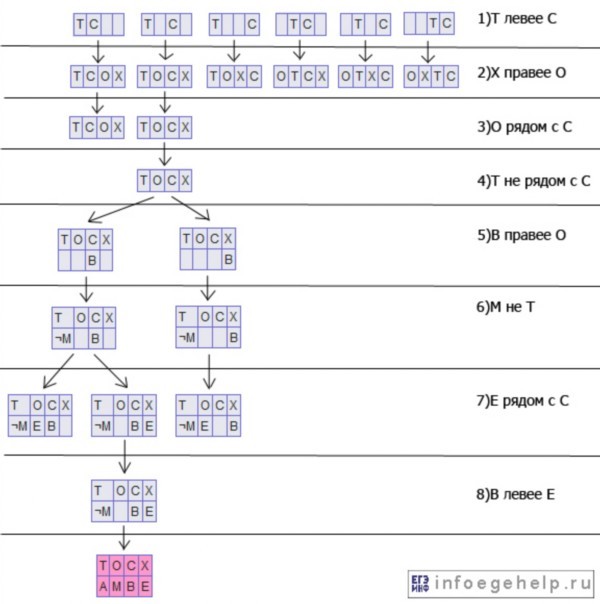
Ответ: АМВЕ